数据结构中的树
树
树(Tree)是一种抽象的数据结构,由节点(Node)和边(Edge)组成,节点之间的边有方向,且没有回路,其中最顶层的节点称为根节点(Root),最底层的节点称为叶子节点(Leaf),其他节点称为内部节点(Internal Node)。
二叉树
满二叉树
满二叉树是一种特殊的二叉树,其中除了叶子节点之外,每个节点都有两个子节点。换句话说,满二叉树是一棵深度为h的二叉树,其中每个层都恰好有 $2^{h-1}$ 个节点。
完全二叉树
完全二叉树是一种二叉树,其中除了最后一层可能不是满的,其它层都是满的,并且在最后一层上,所有节点都靠左对齐。换句话说,对于深度为 h 的完全二叉树,前 h-1 层都是满的,第 h 层从左到右依次填满节点,缺少的位置在右侧不会出现。
如何表示(或者存储)一棵二叉树?
可以用链表和数组两种方式表示和存储一棵二叉树。链表方式是通过指针将每个节点连接起来,数组方式则是使用数组下标来访问每个节点,数组的索引表示节点在二叉树中的位置,而数组元素存储节点的值。
二叉树的遍历
二叉树的遍历是指按照某种次序访问二叉树的所有节点,可以分为三种遍历方式:前序遍历、中序遍历和后序遍历。
- 前序遍历先访问根节点,然后按照左子树、右子树的顺序访问各个节点;
- 中序遍历先访问左子树,然后访问根节点,最后访问右子树;
- 后序遍历先访问左子树,然后访问右子树,最后访问根节点。
- 此外还有层序遍历,它是按照从上到下、从左到右的顺序依次访问每一层的所有节点。
二叉查找树
二叉查找树(Binary Search Tree,BST)是一种特殊的二叉树,它的每个节点最多只有两个子节点,并且左子树中的所有节点的值都小于它的父节点的值,右子树中的所有节点的值都大于它的父节点的值。由于这个特性,BST被广泛应用于查找和排序的算法中,比如二分查找、快速排序等。
平衡二叉查找树
平衡二叉树是为了解决二叉查找树退化成一颗链表的问题而诞生的。平衡树具有如下特点:
- 具有二叉查找树的全部特性
- 每个节点的左子树和右子树的高度差至多等于1
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉查找树,它的每个节点的左右子树的高度差不超过1,这样可以保证树的高度是O(log n),其中n是树中节点的数量。常见的平衡二叉树有红黑树、AVL树、Treap 等,它们的插入和删除操作都需要进行一定的旋转操作来保持平衡。
红黑树
红黑树本质上是对 “2-3-4 树” 的一 种实现。采用标准的二叉查找树节点附着上额外的颜色信息来表示 2-3 树的实现,每一 个红色节点都和它的父亲节点一起,构成了一个 3 节点的模拟,这就是红黑树设计的本质。
红黑树的定义:
- 每个结点是红的或者黑的。
- 根节点是黑色的。
- 每个叶子节点都是黑色的空节点(nil),也就是说,叶子节点不存储数据;
- 相邻的节点不能同时为红色,也就是说,红色节点是被黑色节点隔开的。
- 对每个结点,从该结点到其子孙结点的所有路径上的包含相同数目的黑结点。
- 最长路径 <= 最短路径 * 2
红黑树虽然仅仅做到了近似平衡,而非严格平衡,但其维护平衡所需的成本却比 AVL 树低。此外,红黑树的插入、删除和查找等操作具有稳定的性能。在工程应用中,需要应对各种异常情况,因此我们更倾向于使用这种性能稳定的平衡二叉查找树。
AVL
AVL 树是一种高度平衡的二叉树,每个节点的左右子树的高度差不超过 1,因此在查找时具有高效的性能。但是,AVL 树为了维持这种高度平衡,每次插入、删除都要做调整,需要进行旋转操作来保持平衡,这些操作相对比较复杂、耗时。因此,当数据集合中有频繁的插入、删除操作时,使用 AVL 树的代价就有点高了。
在 AVL 树中,每个节点的平衡因子是它的左子树高度减去右子树高度的差值(或者相反),它的值只能是 -1、0、1。当 AVL 树的平衡因子不满足平衡条件时,需要通过四种旋转操作(左旋、右旋、左右旋、右左旋)来保持平衡。
多叉树
多叉树(Multiway Tree)是一种每个节点可以有多个子节点的树结构。常见的多叉树有B-Tree(BTree)、B+Tree、Trie等。
B-Tree(BTree)
BTree(B-Tree) 被称为自平衡二叉搜索树的实现,因为它在插入或删除节点时,能够自动调整树的结构,保持树的平衡,使得搜索、插入和删除操作的时间复杂度可以保持在 O(log n) 的级别。
多叉 B-Tree 有两个优点:
- 减层高:每个节点可以拥有多个子节点,这种结构能够有效地减少树的深度,从而减少搜索的时间。
- 较少IO:系统从磁盘读取数据到内存时是以磁盘块(block)为基本单位的,位于同一个磁盘块中的数据会被一次性读取出来,而不是需要什么取什么。
B-Tree 在两种特定的情况下最流行:
- 当一个节点中的 key 个数 L(L=2 或 L=3),从概念上讲它是属于简单的平衡树
- 2–3 tree 和 2–3–4 trees,因为它的实现引入了两种异构的节点,导致代码写起来相当复杂,并没有被广泛使用。红黑树是由此树演变而来的。
- 一个节点上的 L 的个数非常多(如上千个)
- 在实践中用于数据库和文件系统(即具有非常大的记录的系统)。
由于 B-Tree 的构造方式,它有两个性质:
- 所有的叶子节点必须与源节点距离相同。
- 一个具有
k个项的非叶子节点必须恰好有k+1个子节点。
2-3 Tree
2-3 Tree 属于 B-Tree。它有一下特点:
- 2-3 Tree是一种三叉树。
- 每个节点包含 1 或 2 个键,所有的非叶节点都有 2 或 3 个子节点(因此得名“2-3 Tree”)。
- 所有的叶子节点都处于同一级别。
- 在插入操作时(都会插入叶子节点),如果一个节点溢出,它将被分成两个节点,中间元素将插入到父节点中(可能会引起一系列的分裂操作)。
- 在删除操作时,如果一个节点下溢,它可以从相邻节点中借取一些元素,或者如果节点很小,则可以合并它们。
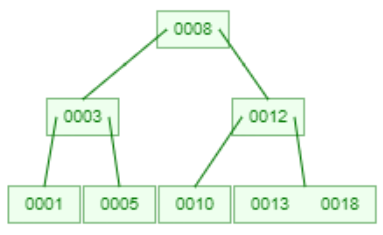
比如:下面是一棵 2-3 Tree:
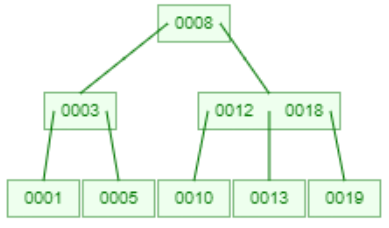
再插入19后,由于在一个节点上有13,18,19了,就把中间的18提上到父节点上面。
2-3-4 Tree
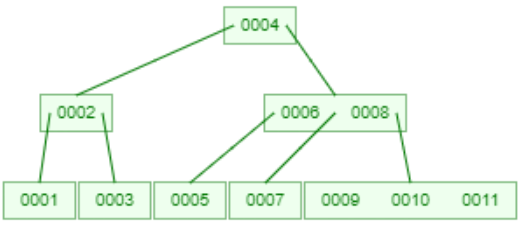
2-3-4 树(也称为 2-4 树)是一种可用于实现字典的自平衡数据结构。和上面的 2-3 Tree 一样的规则,当叶子节点有 4 个元素的时候会上提。
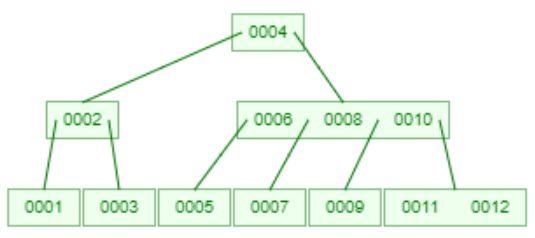
再插入12的时候,会把10提到父节点。
B+Tree
B+tree 与 B-tree 类似,也是一种多路搜索树
- 但是它的所有数据都存储在叶子节点中,而非 B-tree 中的所有节点都可能存储数据。
- B+Tree 的叶子节点和相邻节点是双向链接的。
- B+tree 在插入和删除节点时也能够自动调整树的结构,但是它并不会保持树的完全平衡,而是保持部分平衡,即所有叶子节点位于同一层级,从而使得范围查询等操作更加高效。
- 因为 B+tree 并不是完全平衡的,所以它通常不被称为自平衡二叉搜索树的实现。
Trie Tree
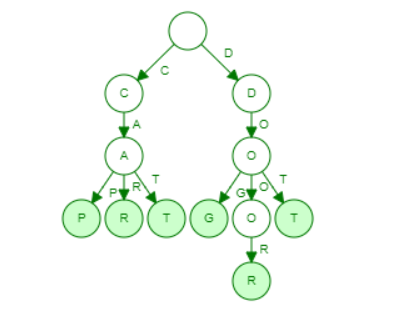
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。通过就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
特点:Trie 树很浪费内存,但是非常高效。
用这些单词来构建Trie 树:‘cat’, ‘car’, ‘cap’, ‘dog’, ‘dot’, ‘door’。